거리와 속도 측정 (3)

파동에서 속도, 파장, 진동수사이의 관계 이해하기

자동차를 타고 가다가 기차 철길 건널목 앞에서 차단기가 내려와 멈춘 적이 있다. 그것도 맨 앞에 서게 되어서 지나가는 화물열차를 바로 눈앞에서 보게 됐다. 미국의 화물열차는 상당히 길기 때문에 상당히 오래 건널목 앞에서 기다려야 하는 상황이었다. 그전에는 한번도 얼마나 많은 차량이 화물열차에 연결되어 있는지 세어본 적이 없어서, 기다리는 지루함도 달랠 겸, 맨 앞의 차량부터 소리내어 세기 시작했다. 일정한 시간 간격으로 지나가는 화물열차의 차량을 박자에 맞춰 세는 것이 흥겨웠던지, 자동차에 같이 타고 있던 사람들이 모두 같이 소리내어 세었다.

그런데 이게 웬일인가? 마지막 차량에서 세는 숫자가 100으로 맞아 떨어지는 것이었다. 순간 신이 났는지 자동차에 타고 있던 모두가 박수를 쳤다. 화물열차에 차량이 몇개나 연결되어 있는지 궁금했었는데 구체적인 숫자가 100개로 맞아 떨어지는 우연이 겹친 순간이었다. 항상 100개의 화물차량이 연결되는 것은 아니겠지만 말이다.

그림 1. 기차 철로 건널목 앞에 서서, 화물열차에 연결되어 지나가는 차량 하나하나를 세었던 당시 상황 – 그날은 화물열차에 연결된 차량의 갯수가 100개로 맞아 떨어졌다.

지나가는 기차에 연결된 차량을 세어 기차 전체 길이와 속도 알아내기
기차가 지나갈때 기차에 연결된 차량을 셀 수 있으면, 몇가지를 정보를 더해 움직이는 기차와 관련된 다른 값들을 계산할 수 있다. 먼저 열차 전체 길이를 직접 재지 않고도 추정해 볼 수 있다. 차량 하나의 길이만 알면, 연결된 차량의 갯수를 곱해 기차 전체의 길이를 계산할 수 있다. 화물차량의 길이가 $20m$ 라고 하면, 이런 차량이 100개 달린 열차 전체의 길이는 $20m \times 100 = 2000m$ 가 된다. 물론 이렇게 추정한 열차의 전체 길이가 정확하려면 차량이 길이가 모두 같아야 한다. 일단은 기차에 연결된 모든 차량의 길이가 같다고 가정하고 다음 단계로 넘어가자.

기차에 연결된 차량의 길이를 알고, 추가로 차량이 얼마나 자주 지나가는지를 알면, 기차가 얼마나 빨리 움직이는 지를 계산할 수 있다. 기차의 속도를 추정할 수 있다는 얘기다. 예를 들어 차량 길이가 앞에서 가정한 것처럼 $20m$이고, 지나가는 열차의 차량을 셀 때 1초에 차량 한 대씩 지나가는 것으로 셌다고 하자.[1] 이 말은 곧 차량의 길이 $20m$가 1초만에 지나갔다는 말이 된다. 기차의 속도는 초속 $20m$가 된다. 만약에 2초에 기차의 차량 하나가 지나간다면 1초 동안에는 차량 반 개만 지나가는 셈이다. 1초에 차량 길이 $20m$의 반인 $10m$가 지나가는 것이니 기차의 속도는 초속 $10m$가 된다. 1초에 차량 2대가 지나가면, 차량 두대의 길이인 $40m$가 지나가게 되어 기차의 속도는 초속 $40m$가 된다.

이렇게 기차 차량의 길이와 차량이 얼마나 자주 지나가는지로 기차의 속도를 계산하는 방법을 간단한 공식으로 표현하면

$$ 기차속도 = \text{차량 길이} \times \text{1초에 지나가는 차량의 수}$$

가 된다.

그런데 기차는 보통 초속이 아닌 시속으로 나타내고, 길이도 미터(m)가 아닌 킬로미터(km)로 나타낸다. 다시 말해 1시간에 몇 km로 달리는가로 기차의 속도를 나타내는 것이 일반적이라는 얘기다. 초속 몇 m인가로 나타낸 속도를 시속 km로 나타내는 방법은 비교적 간단하다. 1시간은 60분이고 1분은 60초이니 1시간은 $60 \times 60 = 3600$초다. 초속 $1m$의 속도는 1초에 $1m$를 움직이는 것이니, 1시간동안에는 $1m$인 3600배인 $3600m$를 움직인다. $1000m$는 $1km$이니 1초에 $3600 \div 1000=3.6km$를 움직인 것이 되어, 초속 $1m$는 시속 $3.6$km가 된다. 다시 말해 초속 몇m인가를 시속 몇km인가로 나타내려면, $3.6$을 곱해야 한다.

$20m$길이의 기차 차량이 1초에 하나씩 지나가는 경우는 초속 $20m$라고 했다. 이를 시속 몇 $km$인 지로 바꾸면 20에 3.6을 곱해야하니 시속 $72km$가 된다. 차량이 2초에 하나씩 지나가는 경우는 초속 $10m$이니 10에 3.6을 곱해 시속 $36km$가 되고, 1초에 차량이 2개씩 지나는 경우는 초속 $40m$이니, 40에 3.6을 곱해 시속 $144km$가 된다.

차량이 얼마나 자주 지나가는지는 전체 차량의 갯수를 세는데 얼마나 걸렸지로도 잴 수 있고, 정해진 시간에 차량 몇대가 지나가는지로도 셀 수 있다. 차량 하나가 지나가는데 걸리는 시간을 잴 수도 있다. 세 경우 모두 약간의 산수만 하면 1초에 차량 몇대가 지나가는지를 알 수 있다. 계산하면, 차량이 얼마나 자주 지나가는지를 알 수 있다. 기차의 속도가 매우 빠른 경우는 기차 차량 전체의 갯수를 세는데 걸리는 시간을 재는 방법이 유리하고, 기차가 매우 느리게 가는 경우는 차량 하나가 지나가는데 걸리는 시간을 재는 것으로 충분할수도 있다.

자동차와 기차의 길이를 잴때 오차 비교: 도로 위를 빠르게 달리는 자동차의 속도를 잴때는 본문에서 설명한 기차 속도를 재는 방법을 사용하기가 곤란하다. 차가 반복되어 연결되어있지 않기 때문이다. 자동차 앞부분에서 뒤부분까지 지나가는데 걸리는 시간을 잰 다음, 자동차 길이를 잰 시간으로 나누면 속도를 계산할 수 있지만, 빨리 달리는 자동차는 그 시간이 매우 짧다. 예를 들어 5m길이의 자동차가 시속 72km (= 초속 20m)로 달릴때, 앞부분에서 뒷부분까지 지나가는데 걸리는 시간은 0.25초에 불과하다. 자동차 앞부분과 뒷부분이 지나가는 순간을 눈으로 보고 스톱워치 버튼을 누르는 시간까지의 반응 시간이 0.05초만되어도 자동차 속도를 계산한 값에는 20%가량의 오차가 발생한다. 반면 같은 속도로 달리는 200m길이의 기차가 앞부분에서 뒷부분까지 지나가는데 걸리는 시간은 10초다. 스톱워치 버튼을 누르는 반응시간도 0.05초로 같다면, 오차는 0.5%정도에 불과하다. 기차의 길이를 잴때의 오차가 40분의 1정도로 훨씬 더 정확함을 알 수 있다.

고속열차, 케이티엑스의 경우
이번에는 한국에서 운행하는 가장 빠른 열차인 케이티엑스(KTX)의 경우를 보자.[2] 최고 속도는 시속 300km에 이른다. 만약에 서울에서 출발하는 부산행 KTX가 쉼없이 전 구간을 최고 속도로 달린다면 1시간 30분 정도면 목적지에 도착할 수 있다. 하지만 중간에 정차하는 역에서 잠시 쉬어야하고, 곡선구간에서는 속도를 줄여야하는 등, 몇 가지 제약 조건이 있기 때문에 부분적으로만 최고 속도를 낼 수 있고 평균 속도는 최고 속도에 못 미친다.

KTX가 최고 속도로 달리는 구간에서 눈앞에 지나가는 KTX의 차량을 센다고 하자. 이때 얼마나 빨리 열차 차량을 세야 할까? 이 문제는 ‘열차의 속도’를 아는 상태에서 ‘1초에 지나가는 차량의 수’를 알아내는 문제다. 같은 속도로 달린다고 해서 차량을 세는 것이 항상 똑같지는 않다. 열차를 구성하는 차량의 길이가 길면 더 천천히 세어야 하고, 차량의 길이가 짧으면 더 빨리 세어야 하기 때문이다. 차량의 길이를 먼저 알아야 ‘1초에 지나가는 차량의 수’를 예측할 수 있다.

KTX 열차는 기관차, 동력객차, 객차로 구성되어 있고, 그중 기관차의 길이는 22.5m , 동력객차의 길이는 21.8m, 객차의 길이는 18.7m라고 한다.[3] 총 20개의 열차 차량 중 80%인 16개의 차량이 객차라고 하니, 객차의 길이를 차량의 길이로 보고 문제를 풀어보겠다.

‘기차 속도’와 ‘차량 길이’를 알고서, ‘1초에 지나가는 차량의 수’를 알아내려면, ‘$기차속도 = \text{차량 길이} \times \text{ 1초에 지나가는 차량의 수}$’를 변형한 공식을 써야 한다. 양쪽을 ‘차량길이’로 나누어 정리하면 아래와 같은 공식이 나온다.

$$\text{1초에 지나가는 차량의 수} = \text{기차 속도} \div \text{차량 길이}$$

‘1초에 지나가는 차량의 수’에 사용된 시간은 초 단위다. 그런데 ‘열차 속도’는 ‘1시간 동안 움직이는 거리’를 나타내는 ‘시속’으로 표현했다. 둘 다 같은 시간 단위로 변환할 필요가 있다. 이번 문제에서는 ‘1초에 지나가는 차량의 수’를 알아내는 것이므로 열차 속도에서 사용한 시속을 ‘1초에 움직인 거리’ 인 ‘초속’으로 바꿔야 한다. 여기에다 ‘열차 속도’에서는 거리를 km로 표현했지만, ‘차량 길이’는 m로 표현했다. 이 둘도 같은 길이 단위로 변환해야 한다. 이 문제에서는 km대신 m로 바꿔보도록 하겠다.

시속 300km는 1시간에 300km를 움직이는 속도다. 1시간이 3600초이고, 1km는 1000m이니 3600초 동안 300000m를 움직인 속도가 된다. 300000m를 3600으로 나누면 1초 동안 움직인 거리는 $300000m \div 3600 = 83.3m$가 된다. 이 값이 바로 초속으로 나타낸 ‘기차 속도’로 초속 83.3m가 된다.

이 두 숫자를 위의 공식에 넣어 계산해보자. $83.3 \div \text{18.7(객차의 길이)} = 4.45$라는 계산 결과가 나온다. 1초에 숫자 차량 네개를 세는 것보다 더 빨리, 하지만 다섯개를 세는 것보다는 더 느리게 세어야 한다. 이렇게 열차의 차량을 센다면, 차량 20대가 연결된 KTX 열차의 열차 맨 앞 차량부터 맨 뒤 차량까지 세는 데 불과 5초도 안 걸린다. 상당히 빨리 세어야 하기 때문에 실수하지 않고 세기가 쉽지 않을 듯하다.

‘기차 속도’와 ‘1초에 지나가는 차량의 수’를 알고서, ‘차량 길이’를 알아내려면, ‘기차속도 = 차량 길이 × 1초에 지나가는 차량의 수’를 변형한 공식을 써야 한다. 양쪽을 ‘1초에 지나가는 차량의 수’로 나누어 정리하면 아래와 같은 공식이 나온다.

$$\text{차량 길이} = \text{기차속도} \div \text{ 1초에 지나가는 차량의 수}$$

결과적으로 기차의 속도, 기차에 연결된 차량 각각의 길이, 그리고 그 차량이 얼마나 자주 지나가는지 일허게 세가지 값사이에는 세개의 공식이 가능하다. 다시 말해 세개의 값들은 얽혀 있어서, 셋중에 두개의 값만 알면 나머지 하나의 값을 계산할 수 있는 관계임을 알 수 있다.

기차를 물결로 보고 하는 계산
기차의 예를 살펴봄으로써 우리는 물결모양의 움직임, 다시 말해 “파동”의 기본적인 성질을 알아볼 준비가 됐다.

이제 아래 그림과 같이 정지된 순간의 물결 모양을 보자. 물결 모양의 가장 높은 곳을 ‘마루’라고 부르고 가장 낮은 곳을 ‘골’이라고 부른다. 골을 기차의 경우에서 차량과 차량이 연결된 부분이라고 하면, 마루는 차량의 중간 부분에 해당한다. 인접한 골사이의 거리 또는 마루사이의 거리는 기차의 차량 길이에 해당하는 ‘기본 모양의 길이’가 된다. 이 ‘기본 모양의 거리’가 일정할 경우, 인접한 골사이의 거리 또는 마루사이의 거리를 ‘물결 사이의 길이’를 의미하는 ‘파장’이라고 부른다.

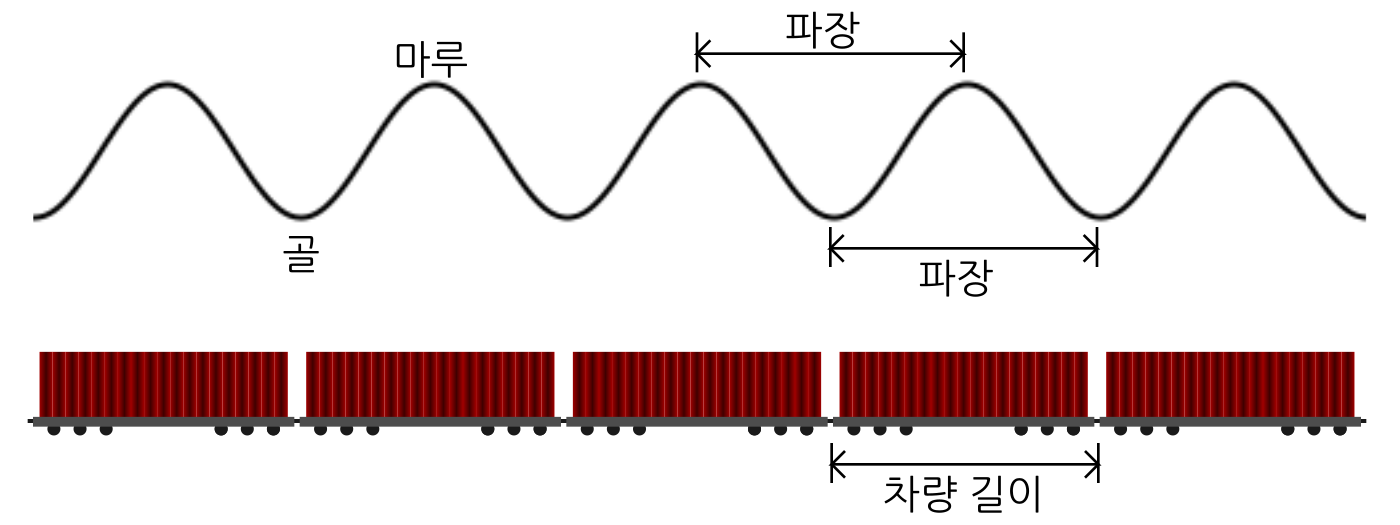
그림 2. 물결 모양과 화물열차 비교: 차량의 길이를 물결 모양에서 인접 마루 사이의 거리 또는 골 사이의 거리인 ‘파장’과 비교할 수 있다. 물결 모양이 움직이는 경우에, 위치 한 곳을 정해서 1초 동안 지나가는 마루(또는 골)를 세면 이 갯수가 ‘진동수’(또는 주파수)가 된다.

한쪽 방향으로 움직이는 물결 모양을 생각해 보자. 파장은 물결 전체에 걸쳐 변하지 않는다고 가정하자. 고정된 한 지점을 기준으로 물결 모양의 마루 또는 골이 1초에 몇 번씩 지나가는지를 잴 수 있다. 이렇게 한 지점에서 정해진 시간에 물결이 몇 번 반복되느냐(또는 지나가느냐)를 ‘진동수’ 또는 ‘주파수’라고 부른다. 보통 1초에 몇 번 반복되는 횟수로 나타내고, 단위는 ‘헤르츠(Hz)’를 쓴다. 1초에 1번 반복되면 1헤르츠(1Hz), 10번 반복되면 10헤르츠(10Hz), 100번 반복되는 100헤르츠(100Hz)가 진동수 값이 된다.

파동에 적용
이제 열차의 경우에서 계산했던 것을 그대로 움직이는 물결모양에 적용해보자.　일단 인접 마루 사이 거리가 1m라고 하고, 한 지점에서 1초 동안에 물결 모양이 하나씩 지나간다고 하자. 1초에 1m가 하나씩 지나가니 속도는 초속 1m가 된다. 다시 말하면 파장이 1m이고 진동수가 1Hz여서, 물결 모양이 움직이는 속도는 초속 1m인 경우다.

마루 사이의 거리가 멀어져 2m고 마루가 1초 동안에 2개씩 지나가는 경우는 어떨까? 1초에 2m가 2개씩 다시 말해 4m가 지나가므로 물결 모양이 움직이는 속도는 초속 4m가 된다. 파장이 2m이고 진동수가 2Hz여서 물결 모양이 움직이는 속도가 초속 4m인 경우다.

위의 예를 통해서, 우리는 파장, 진동수, 속도 사이에 다음과 같은 관계가 있음을 알 수 있다.

$$속도=파장 \times 진동수$$

표현에 사용된 단어만 바뀌었을 뿐, 기차의 속도를 계산하는 데 사용한 ‘기차속도 = 차량 길이 × 1초에 지나가는 차량의 수’ 공식과 다를 바가 없다. 위의 공식을 이용하면 더 복잡한 경우에도 속도를 쉽게 계산할 수 있다. 예를 들면 파장이 0.17m(=17cm)이고 진동수가 2000Hz (1초에 2000번 반복됨)인 물결 모양 움직임의 속도는 초속 0.17 × 2000 = 340m가 됨을 알 수 있다. 공기중에서 특정 음높이 소리의 속도가 이렇다.

물결 모양의 경우도 마찬가지로 파장, 속도, 진동수 이렇게 셋중에 둘만 알면 나머지 하나를 계산할 수 있다. 속도와 진동수를 가지고 파장을 알아내려면,

$$ 파장=속도 \div 진동수$$

수식을 사용하면 되고, 속도와 파장을 가지고 진동수를 알아내려면,

$$ 진동수=속도 \div 파장 $$

수식을 사용하면 된다.

물결 모양의 움직임인 ‘파동’은 물리학 뿐만아니라 다른 과학분야에도 많이 나오는 용어다. 파동에 대해서 말할때는 파장, 진동수, 그리고 속도를 항상 거론한다. 이 세가지 양은 앞에서 표현한 세개의 관계식으로 비교적 단순하게 서로 얽혀있다. 말이 세개의 관계식이지 셋중에 두개의 수식은 나머지 하나의 수식에서부터 이끌어낼 수 있다. 그래서 하나의 수식, 보통은 ‘속도=파장×진동수’를 기본으로 알고 있으면 된다.

퀴즈:

(1) 음악의 박자를 맞추는데 사용하는 메트로놈(metronome)이 1분에 120번 소리를 낸다. 1초에는 몇번 소리를 낼까?
(2) 소리는 공기중에서 초속 340m로 날아간다. 진동수가 10000 Hz인 소리의 파장은 얼마일까?
(3) 군대가 행군을 할때 앞렬과 뒷렬사이의 거리를 1.5m로 유지한채 일정한 속도로 걸어가고 있다. 도착선(finish line)에 5초에 3개의 열이 통과한다고 할때 군인들이 걸어가는 속도는 얼마일까?

주.

[1] 100개의 차량이 연결된 화물열차라면 기차 맨 앞부분에서 맨 뒷부분까지 지나가는데 걸리는 시간은 100초였을 것이다. 하지만 처음 차량 숫자 1을 센 순간부터 마지막 차량 숫자 10을 센 순간까지의 시간 차이로 본다면 99초가 되겠다. 1과 100의 차이는 99이기 때문이다.
[2] KTX의 원조 격인 프랑스의 테제베(TGV)는 Train a Grande vitesse라는 프랑스 말의 줄임말로 말 그대로 ‘고속열차’라는 뜻이다. 독일의 고속열차는 ICE (InterCity-Express), 일본의 고속철도는 신간센(新幹線)이라 불린다.
[3] KTX-I https://ko.wikipedia.org/wiki/KTX-I