쌓인 상자 갯수 세기에서 나노 촉매로 에너지 장벽 낮추기까지
그림 1의 윗렬의 맨왼쪽과 같이 상자 하나만 달랑 놓여 있는 경우를 보자. 편의상 박스는 정육면체라고 하자. 박스 대신 주사위라고도 생각해도 되겠다. 이 상자는 당연히 외부에 노출된다. 그 옆의 그림처럼 상자 네 개를 네모 모양으로 정렬하고 이를 2층으로 쌓은 상자 더미를 만들어보자. 가로, 세로, 높이 방향으로 길이가 두배씩 늘어 상자의 총갯수는 $2\times 2 \times 2=2^3=8$개의 상자가 쌓인다. 이 경우도 모든 상자가 외부에 노출되어 있다.
상자 쌓기, 그리고 상자 갯수 세기
상자를 한 면에 $3\times 3=9$ 개씩 정렬하고 이를 3층으로 쌓은 상자 더미를 만들어보자. 이 상자 더미 속에 있는 상자의 총 갯수는 $3 \times 3 \times 3=3^3=27$ 개다. (그림 1 왼쪽에서 세 번째). 2개의 상자가 전혀 볼 수 없는 위치에 있다. 하나는 상자 더미 내부 중간에 위치한 상자이고, 또다른 상자는 바닥과 접한 면의 가운데에 있는 상자다. 만약 상자들이 서로 잘 달라붙어 있고 상자 더미를 들어올릴 수 있으면 바닥면의 가운데에 있는 면도 외부에 노출되어 볼 수 있으니, 내부 중간에 있는 상자 하나만 외부에 노출되지 않은 상자로 볼 수 있다.
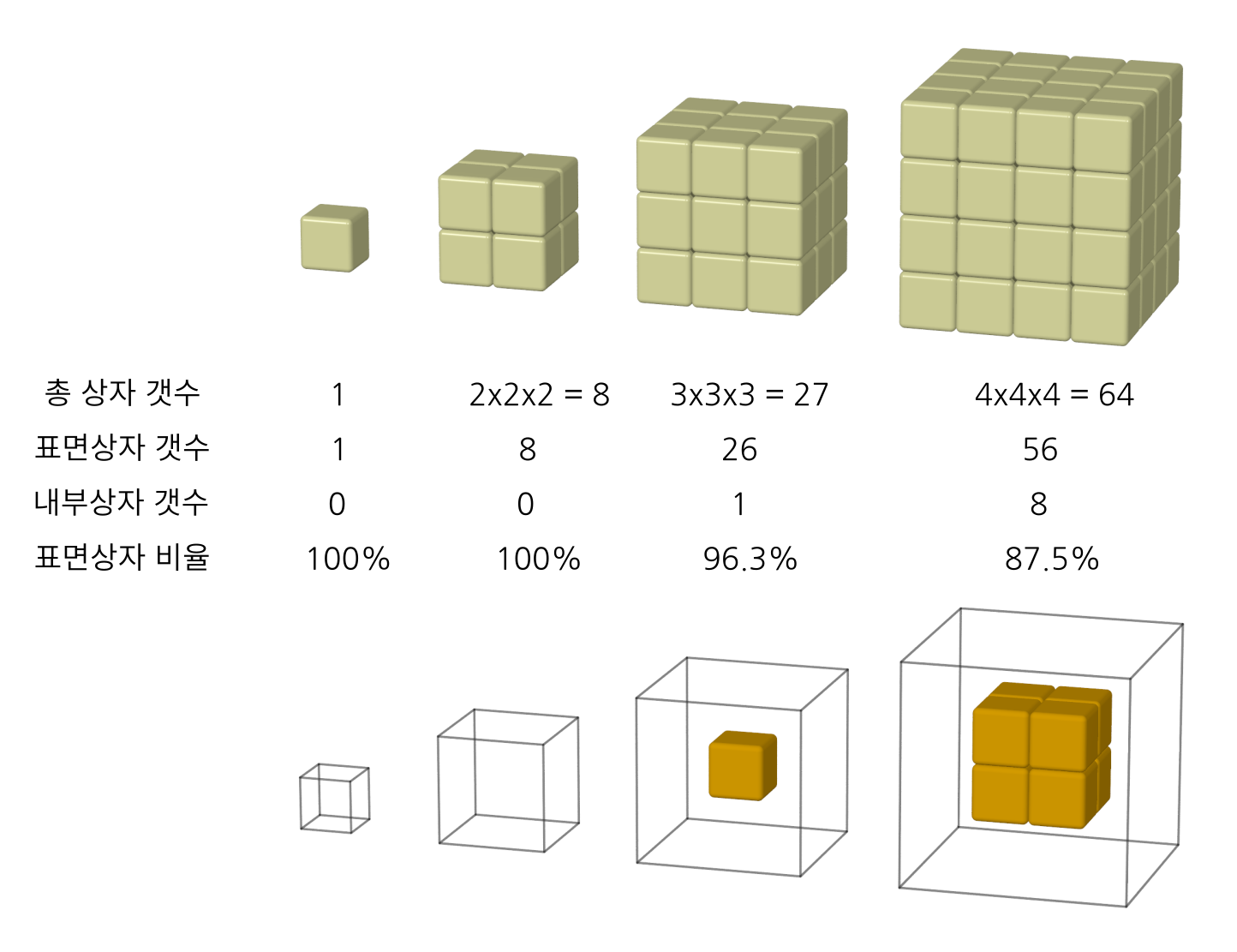
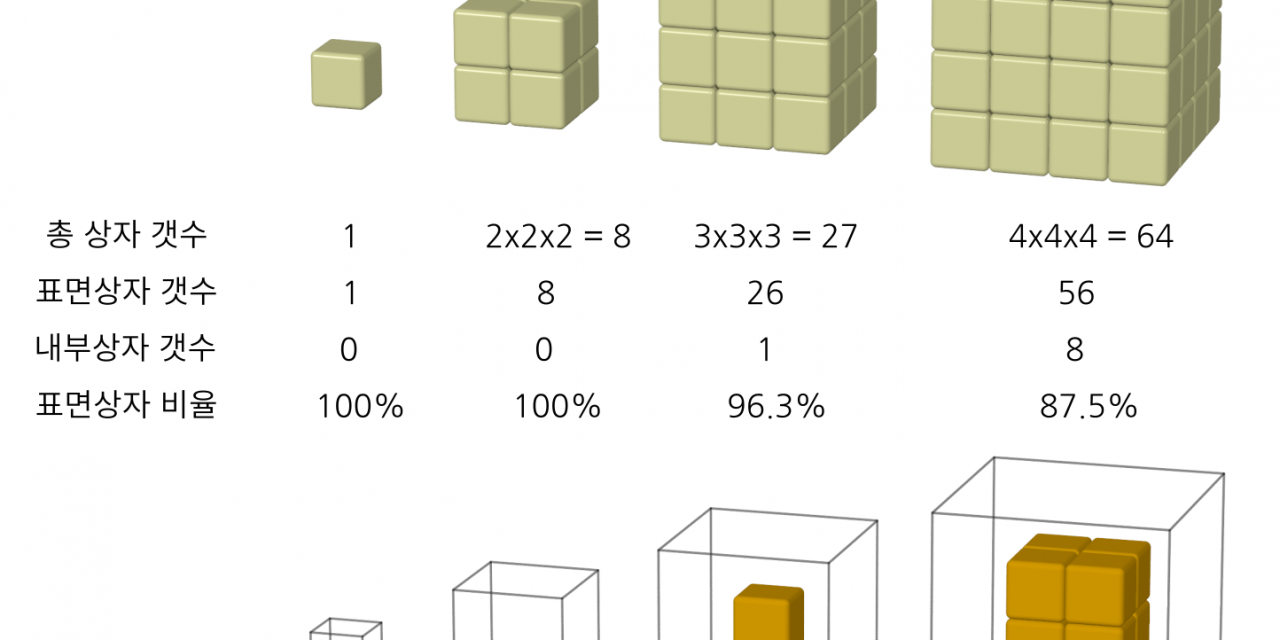
그림1. 상자 쌓기, 그리고 상자 갯수 세기. 표면상자는 상자들이 놓인 바닥을 포함해서 외부에 노출된 상자이고, 그외의 상자 더미 내부에 있는 상자가 내부 상자다. 맨 아래 그림은 상자 더미 안에서 속에 감춰져 밖에서 보이지 않는 상자들을 따로 그렸다.
외부에 노출되지 않은 상자는 내부에 위치하니까 ‘내부상자’라고 부르고, 외부에 노출된 상자는 표면에 위치하고 있으니까 ‘표면상자’라고 부르자. 일단은 상자가 쌓여있는 바닥과 바로 맞닿는 상자도 표면상자에 포함하는 것으로 하자. 상자가 달랑 하나만 있는 경우와 $2 \times 2 \times 2=8$ 개의 상자를 쌓은 경우는 100% 모두 표면 상자다. 하지만 $3 \times 3 \times 3=27$ 개의 상자를 쌓은 경우는 26개가 표면 상자이어서 ‘총 상자 갯수’ 대비 ‘표면상자 갯수’의 비율은 26/27 = 0.963(96.3%)이다. 1(100%)에 가까우면 표면상자가 대부분임을 의미하고 0(0%)에 가까우면 내부원자가 대부분임을 의미한다. 표면상자 비율이 0.963 (96.3%)이니, 거의 대부분이 표면상자라고 보면 되겠다.
더 크게 쌓아 그림 1의 맨 오른쪽처럼 $4 \times 4 \times 4=64$ 개의 상자를 쌓은 경우도 내부상자와 표면상자의 갯수를 세어보자. 눈에 보이는 표면상자를 먼저 세어봐야 하겠다. 각각의 면이 마주치는 부분인 모서리에 걸쳐 있는 상자들은 중복되어 셀 수 있으니 주의해야 한다. 56개의 표면상자가 있다. 그럼 내부상자의 갯수는 총 상자의 갯수에서 표면상자의 갯수를 뺀 8개다. 이 경우 총 상자 갯수 대비 표면상자 갯수의 비율은 56/64 = 0.875이다. 비율이 27개의 상자 더미에 비해 좀 줄어들었다.
더 큰 상자 더미는 일일히 표면상자의 갯수를 세기가 너무 번거로울 수 있다. 지금까지 크기가 다른 상자 더미에서 표면상자와 내부상자의 갯수를 세면서 눈치챘겠지만, 내부상자의 갯수는 한 모서리의 길이가 상자 2개 길이 만큼 줄어든 정육면체 더미에 있는 상자의 갯수다. 한 예로 $4 \times 4 \times 4=64$ 개의 상자더미의 내부상자 더미는 모서리 길이가 2씩 준 $2 \times 2 \times 2=8$개의 상자로 만들어졌다. 표면 상자의 갯수는 전체 상자의 갯수에서 이 내부상자의 갯수만 빼면 된다. 계산하면 표면상자 갯수는 $4 \times 4 \times 4-2 \times 2 \times 2=64-8=56$개다.
이 방법을 한 모서리의 길이가 10상자가 늘어선 길이인 정육면체 상자 더미에 적용해보자. 한면에 $10 \times 10=100$개의 상자가 10층이 쌓여 있으니 총 $10 \times 10 \times 10=1000$ 개의 상자가 쌓여있다 (그림 2). 내부상자는 모서리 길이가 두 개의 상자 길이만큼 줄어든 여덟 상자의 길이인 내부상자 더미에 있다. 계산하면 내부상자의 갯수는 $8 \times 8 \times 8 = 512$ 개가 된다. 표면상자 갯수는 전체 상자수에서 내부상자의 갯수를 뺀 488개가 되어, 전체 상자에서 표면상자가 차지하는 비율은 488/1000 = 0.488이다. 거의 반만 표면상자일 만큼 비율이 많이 줄었다.
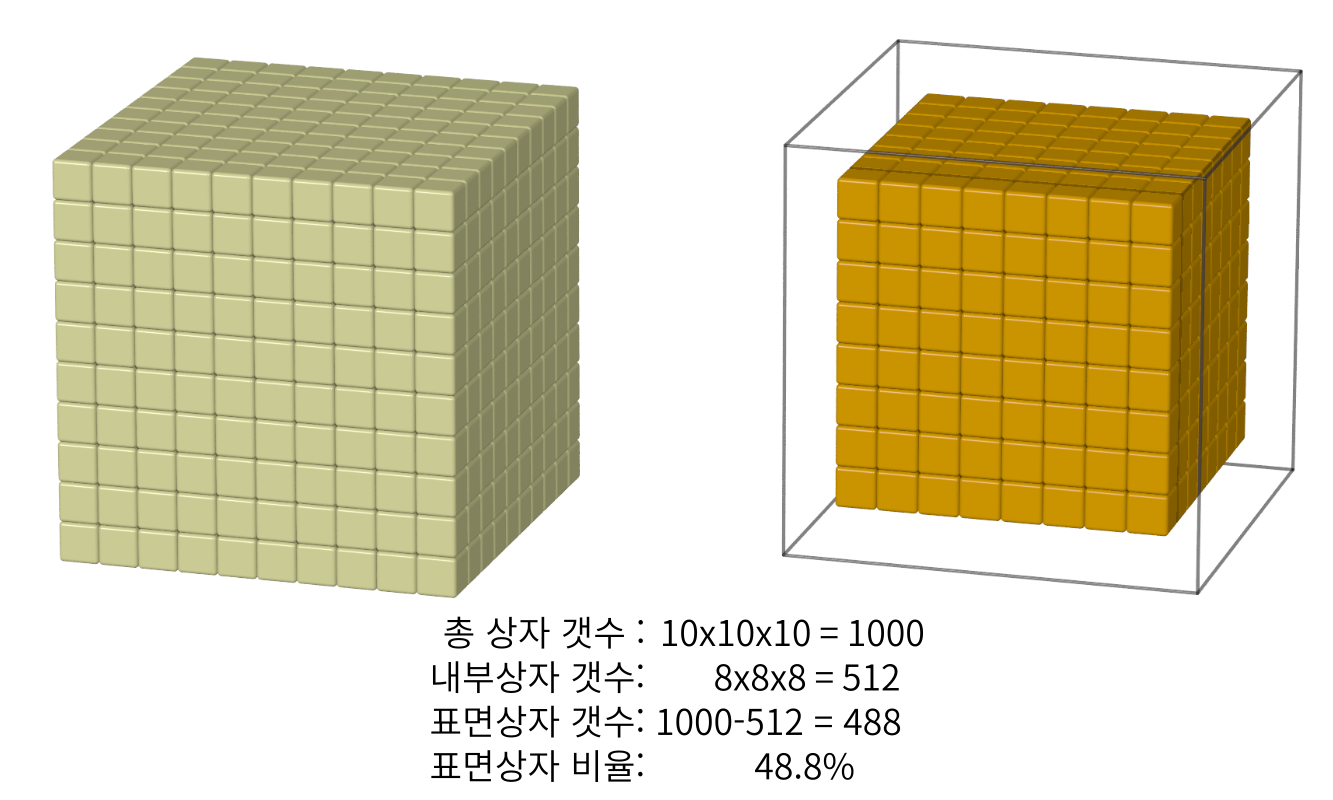
그림 2. 상자 1000개(10×10×10)를 쌓았을 때 표면상자의 갯수와 비율
만약에 100×100×100 = 백만 개의 상자를 쌓은 경우에는 내부상자의 갯수는 98×98×98 = 94,1192 개이고 표면상자의 갯수는 1000000 – 941192 = 58808 개다. 표면상자의 비율은 0.05888로 떨어진다. 얼추 20개 상자 중에 한 상자만 표면상자다. 상자를 크게 쌓으면 쌓을수록 표면 상자의 비율이 줄어드는 것을 알 수 있다.
원자 덩어리에서 원자 갯수 세기
이제 각각의 상자를 원자라고 생각해보자. 내부상자와 표면상자도 마찬가지로 ‘내부원자’와 ‘표면원자’가 된다. 원자의 크기가 대략 0.3nm(나노미터: 머리카락 굵기의 10만 분의 1)이니, 3×3×3=27 개의 원자를 쌓은 덩어리의 한쪽 모서리의 길이는 0.9nm 정도로 1nm가 채 안 된다. 이 경우 하나를 뺀 26개의 원자가 표면원자다. 하지만 100×100×100 = 백만 개의 원자를 쌓은 덩어리는 크기가 30nm인데 표면원자의 비율은 6%가 채 안 된다. 눈에 보일랑 말랑한 크기인 머리카락 굵기 0.1mm(밀리미터) 크기 만큼 원자를 쌓으면 표면원자의 비율은 대략 0.002%, 다시 말해 ‘10만 개 원자 중 고작 2개’만이 표면원자가 된다.
실제 원자의 세계에서는 위와 같이 상자를 쌓는 방식과는 다른 방법으로 원자가 쌓이는 경우가 대부분이다. 가장 조밀한 방식으로 쌓은 면심 입방 (face-centered cubic: fcc) 구조가 대표적인데, 이때 입자의 모양은 둥근 공 모양에 가깝다 (그림 3). 공 모양일 때 표면의 면적이 가장 작은 것을 감안하면, 전체 원자의 갯수가 같을때는 이왕이면 둥근 공모양에 가까울수록 표면원자 비율이 더 작아짐을 알 수 있다. 이 경우에도 입자의 크기가 작을수록 표면원자 비율이 더 커진다는 사실은 변함없다.
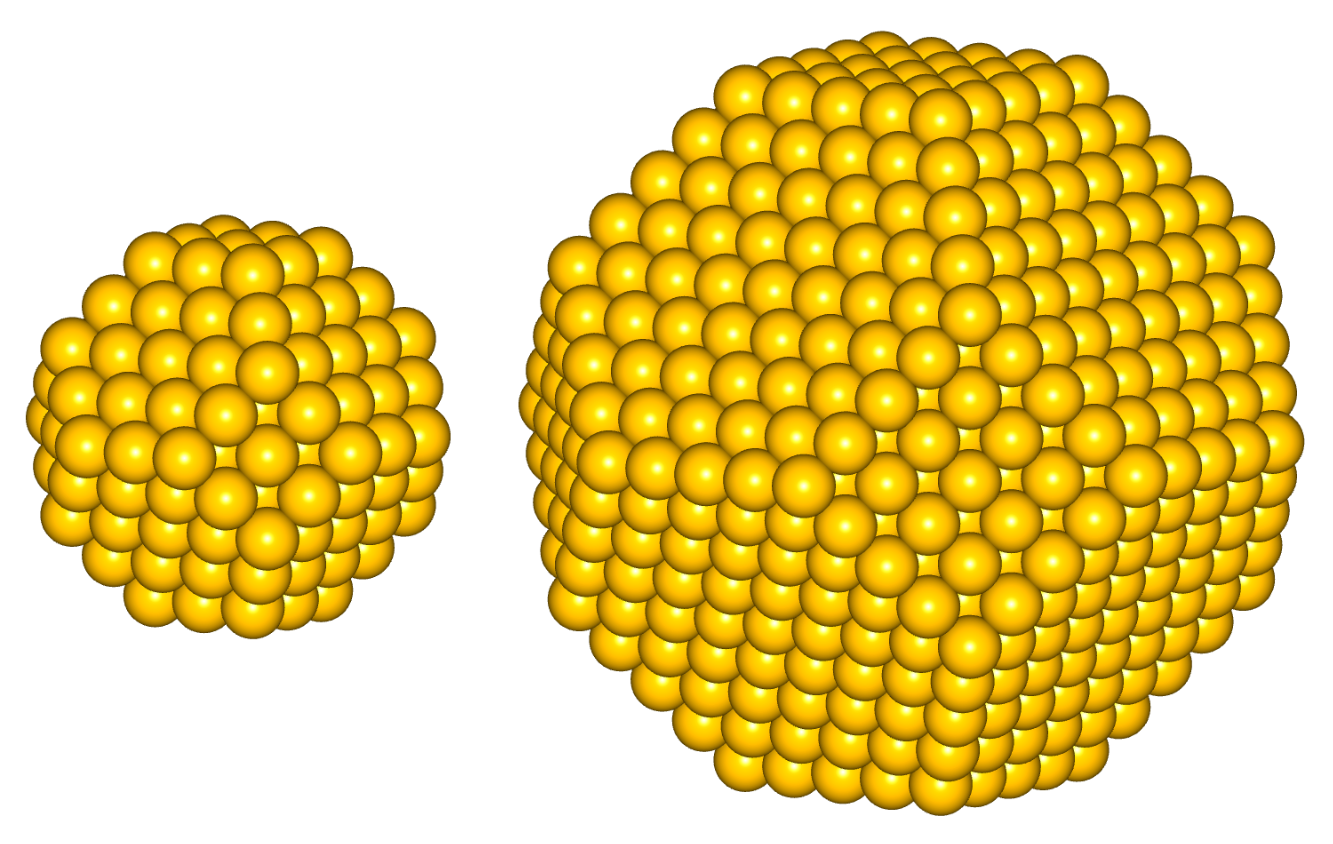
그림 3. 실제 원자가 쌓이는 방식에서 예상해볼 수 있는 둥근 모양: 깎인 정팔면체 (truncated octahedron)
이렇게 표면원자의 비율을 계산할 수 있게 되면, 이 글의 제목에 나와 있는 나노촉매, 즉 나노미터 크기 촉매의 중요한 성질 하나를 이해할 수 있는 준비가 된다. 그런데 촉매는 뭘까? 촉매는 화학반응에 관여하는 물질이다. 따라서 촉매에 대해 알려면, 먼저 화학반응을 알아볼 필요가 있다.
다른 물질을 만드는 화학반응
화학반응은 어떤 물질이 전혀 다른 물질로 변하는 현상이다. 의약품, 플라스틱을 만드는 것과 같이 자연에 존재하지 않는 물질을 인공적으로 만들어내는 화학반응도 있고, 광합성, 음식물 소화, 더 나아가 생물체가 만들어지는 것 등과 같이 자연적으로 일어나는 화학반응도 있다.
타고, 변질되고, 녹이 스는 것과 같이 단순히 물질을 외부에 노출하거나 다른 물질과 섞는 것만으로는 쉽게 화학반응이 일어나는 경우들도 있다. 하지만 화학반응이 쉽게 일어나지 않는 경우도 많다. 화학반응이 잘 일어나기도 하고 잘 안 일어나기도 하는 것은 화학반응의 길목을 가로막고 있는 장벽(또는 장애물) 때문이다.
우리가 어느 목적지로 간다고 하자. 목적지는 가는 길이 평지에 있다면 걸어서 쉽게 목적지에 도달할 수 있다. 만약에 목적지까지 가는 길에 높은 산이 하나 또는 여러 개가 있고 이 산을 넘어가는 길만 있다고 하자. 어서 목적지까지 걸어 가기가 쉽지 않을 수 있다. 산이 너무 높거나 많으면, 자동차를 타고 산을 넘으면 좀 더 쉽게 목적지에 도달할 수 있다. 여기에서 목적지에 도달하는 것은 화학반응이 일어나는 것으로 보고, 산은 화학반응의 길목에 있는 장벽이라고 보면, 화학반응과 장벽을 이해하는 데 도움이 된다.
화학반응에서 장벽은 에너지로 만들어진 장벽이라, “에너지 장벽”이라고 부른다. 화학반응이 일어나고 안 일어나고는 이 에너지 장벽을 넘기 쉬우냐 어려우냐에 달려 있다. 그런데 화학반응마다 에너지 장벽의 높이와 갯수가 다 다르다. 낮은 산을 쉽게 걸어 넘어갈 수 있는 것처럼, 에너지 장벽이 낮으면 화학반응도 그만큼 쉽게 일어난다. 반대로 산이 높으면 넘어가기 어려운 것처럼, 에너지 장벽이 높으면 화학반응이 잘 일어나지 않는다. 에너지 장벽이 높은 만큼 많은 에너지를 인위적으로 공급해야 장벽을 넘어 화학반응이 일어나게 할 수있다. 주로 열과 압력을 가하는 방법으로 에너지를 공급한다. 높은 산을 넘어갈때 걷는 대신 자동차를 타고 넘어가는 것에 비유할 수 있다.
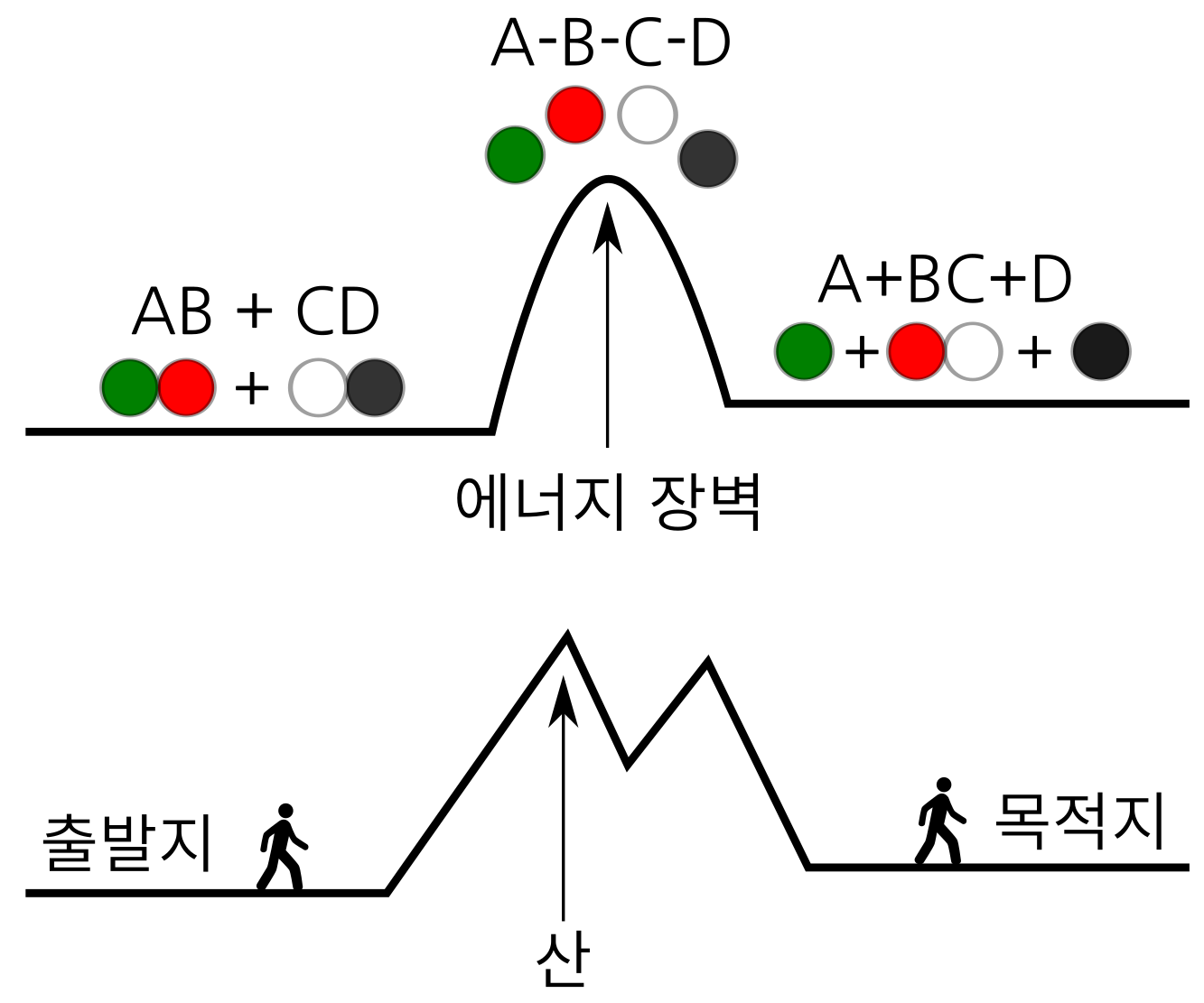
그림 4. 화학반응에서의 에너지 장벽과 목적지까지 가는 길에 있는 산과 비유한 그림
산이 높으면 높을수록 산을 넘는 자동차에 사용되는 에너지인 연료를 더 많이 사용해야 하기에 그만큼 더 많은 비용이 든다. 비슷한 이치로 에너지 장벽이 높는 화학반응일수록 더 높은 열과 압력을 가해야 하기 때문에 더 많은 비용이 들어간다. 에너지 장벽이 지나치게 높으면, 열과 압력을 견뎌내는 생산시설을 만드는 비용이 많이 증가한다.
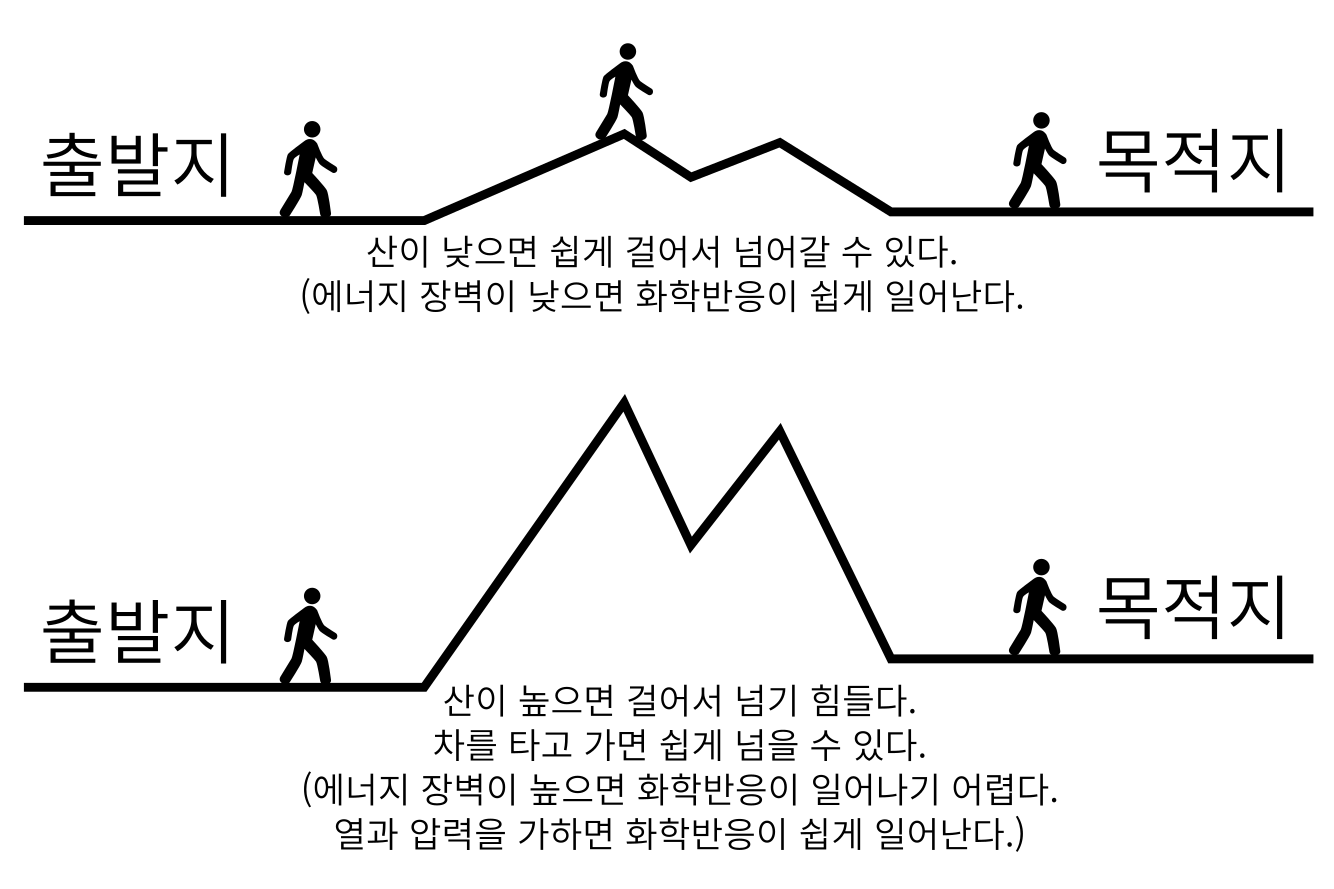
그림 5. 목적지로 가는 도중에 있는 산의 높이가 어떠하냐에 따라 목적지에 걸어서 도달하기가 쉬울 수도 어려울 수도 있다. 화학반응도 마찬가지로 에너지 장벽의 높이가 어떠하냐에 따라 화학반응이 쉽게 일어날 수도 있고 잘 일어나지 않을 수도 있다.
에너지 장벽을 낮추는 촉매: 입자 크기에 따라 달라지는 효율
그런데, 여기에서 “촉매”라는 마법의 물질이 등장한다. 에너지 장벽을 낮춰 화학반응이 더 잘 일어나게 하는 물질이다. 촉매 자신은 화학반응 중에 소모되지 않고 계속 남아있으면서 지속적으로 화학반응의 에너지 장벽을 낮춘다. 에너지 장벽이 낮아지면, 열과 압력을 덜 가해도 화학반응이 일어나니 그만큼 생산비용도 줄일 수 있다. 에너지 장벽을 산에 비유한 것에 적용하면, 촉매가 하는 일은 마치 산의 높이을 낮추는 것과 같다. 산의 높이가 낮아지니 산을 넘기 위해 사용하는 자동차 연료도 그만큼 절약할 수 있고 심지어 아예 아무것도 타지 않고 걸어서도 쉽게 산을 넘을 수 있게 되어 너도나도 산을 넘어 목적지에 도달할 수 있다. 마찬가지로 화학반응에서 촉매가 에너지 장벽을 낮추면 열이나 압력을 덜 가하거나 아얘 가하지도 않고도 화학반응이 일어나게 할 수도 있다.
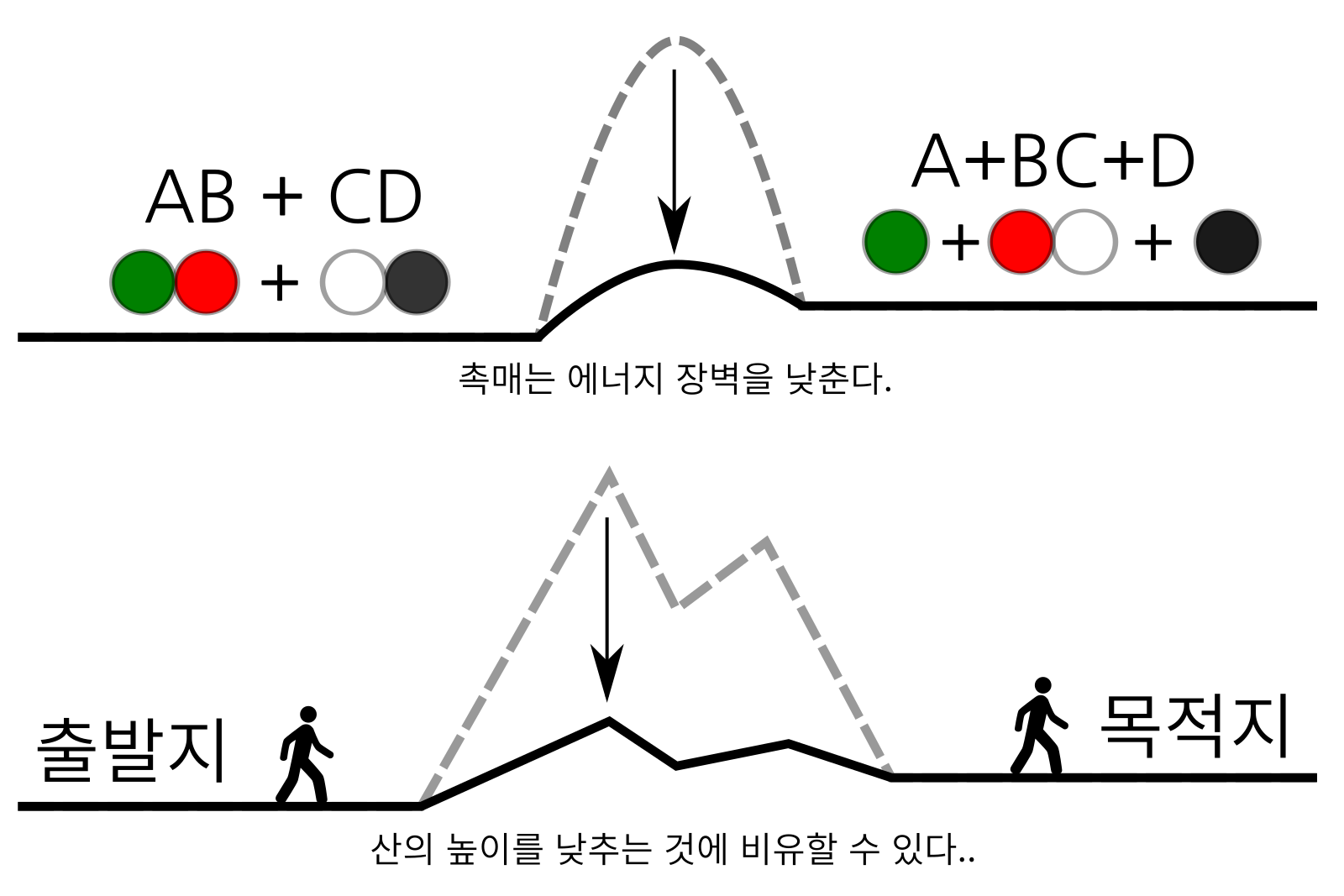
그림 6. 화학반응에서 에너지를 낮추는 것은 비유에서 산의 높이를 낮추는 것에 비유할 수 있다. 산의 높이가 낮아지면 산을 쉽게 넘에 목적지에 도달할 수 있는 것처럼, 에너지 장벽이 낮아지면 쉽게 화학반을이 일어난다.
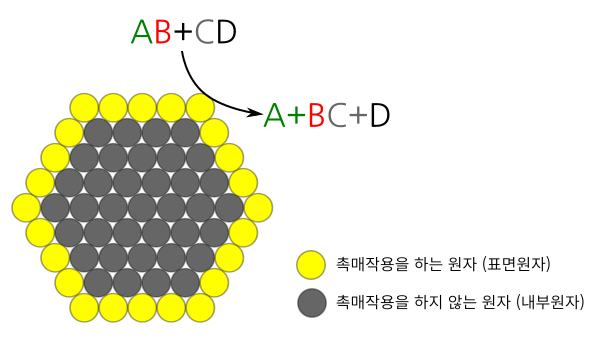
그림 7. 촉매에 있는 원자들중에 촉매작용을 하는 원자들은 주로 화학반응에 노출되는 표면원자들이다. 내부원자들을 표면원자들에 둘려쌓여있기때문에 화학반응에 잘 노출되지 않아 촉매작용을 거의 안한다.
촉매가 고체 상태이면 주로 촉매의 표면에 있는 원자들이 화학반응에 노출되면서 화학반응에 관여한다. 화학반응을 돕기만 하고 소모되지 않기 때문에 촉매 표면에 있는 원자들은 대부분 화학반응 뒤에도 표면에 남게 된다. 반면 표면 안쪽에 있는 내부원자들은 표면원자들로 둘러 쌓여있어서 화학반응에 잘 노출되지 않아 촉매작용을 별로 하지 못한다. 표면원자들이 자리를 옮기지 않으면 내부원자들은 화학반응에 노출되지 않아 촉매로서 작용하기도 어렵다.
자, 이제 눈에 보일랑 말랑한 머리카락 굵기인 0.1mm 크기 고체 상태의 촉매를 생각해 보자. 정육면체 덩어리면 표면원자가 대략 전체 원자의 10만 분의 2이라고 했다. 표면원자가 촉매로 작용한다고 했으니, 전체 원자중의 극히 일부만 촉매 작용에 사용되는 셈이다. 촉매 효율이 엄청나게 낮은 것이다. 면심 입방(fcc) 구조로 공 모양을 하고 있어도 결과는 비슷하다.
그러면 같은 양의 촉매 물질로 어떻게 촉매 효율을 높일 수 있을까?
앞에서 상자또는 원자 쌓는 것으로 확인했듯이 촉매를 아주 작게 만들면 된다. 작으면 작을수록 전체 원자에서 표면원자 갯수의 비율이 커진다. 그만큼 많은 원자들이 촉매 작용에 참여해 촉매 효율이 커진다. 가로, 세로, 높이 각각 10개의 원자가 늘어선 정육면체 나노 클러스터라면 한변의 길이가 대략 30nm인 나노 클러스터다. 초 원자의 원자의 총갯수는 백만개다. 표면원자의 비율은 전체 원자의 6%정도다. 이론상 100개의 원자 중에 6개의 원자 꼴로 촉매 작용을 한다는 얘기다. 나노 클러스터가 공 모양일때는 약간 작아자지만 거의 같은 비율로 촉매 작용을 한다. 크기가 1nm나 그 이하까지 작아지면 거의 대부분이 표면원자가 되어 촉매 효율의 극대화를 기대해볼 수 있다.
나노 크기에서 일어나는 독특한 변화
나노미터 크기로 입자를 만든다고 다 촉매로 사용할 수 있는 것은 아니다. 에너지 장벽이 충분히 낮아지지 않으면 여전히 열이나 압력을 가해야 하고, 이런 상황에서는 나노미터 크기의 입자가 화학반응 중에 모양과 크기를 유지한다는 보장이 없다. 온도가 높으면 표면에 있는 원자들이 떨어져 나가기도 하고, 나노 입자 자체가 퍼지거나 움직이기도 하면서 다른 나노입자들과 합쳐지는등 원래의 크기와 모양을 잃어버리기 쉽기 때문이다.
1nm 크기에 이르면 촉매의 화학적 성질 자체가 달라지기도 한다. 에너지 장벽을 낮추는 정도가 커질 수도 작아질 수도 있다. 에너지 장벽을 더 낮추는 경우는 그만큼 촉매로서 장점이 더 커진다. 심지어는 눈으로 볼 수 있는 크기에서는 촉매로 사용할 수 없다가, 나노미터 크기에 이르면 촉매로 사용할 수 있는 경우도 있다. 금(gold)이 그런 경우다.
나노미터 크기에서는 화학반응 중에 촉매 입자의 구조가 더 유연하게 변하기도 하는데, 이런 구조의 유연성이 때때로 에너지 장벽을 낮추는 데 한 몫 한다. 여러 개의 다른 화학반응이 함께 일어날 때에는, 나노 입자의 크기에 따라 각각의 화학반응에 다르게 촉매 작용이 나타나기도 한다. 이런 경우는 나노 촉매의 크기로 최종 화합물을 선택적으로 조절하는 것이 가능하다.
에탄(ethane)을 만드는 화학반응에서 백금(platinum) 나노 클러스터가 어떻게 촉매 작용을 하는지 연구한 결과를 보면, 나노클러스터의 크기가 원자 10개 일때부터 백금 나노 입자가 에탄 생성 화학반응에 효과적으로 촉매 반응을 하고, 나노 클러스터의 크기가 원자 하나의 차이로 달라지면 구체적인 촉매 작용도 달라진다. 백금 단일 원자가 기존 백금 촉매와는 다른 독특한 촉매 성질을 보인다는 연구 결과도 있다. 나노미터나 그보다 작은 크기에서는 촉매물질의 성질이 독특하게 변한다는 것을 밝혔다는 것에서 이 연구결과들의 의미를 찾을 수 있다.
나노미터 크기에 이르러 새롭게 나타날 수 있는 이런 성질의 변화는 예측하기가 쉽지 않다. 크기가 줄어들면서 변하는 성질의 연장선상에 있지 않은 경우가 많기 때문이다. 그만큼 도전의 가치는 커진다. 이 점은 촉매에 한정되지 않고 다른 나노과학 분야에도 마찬가지다. 많은 연구 그룹이 나노과학 분야 연구에 매진하고 있는 이유의 하나다.
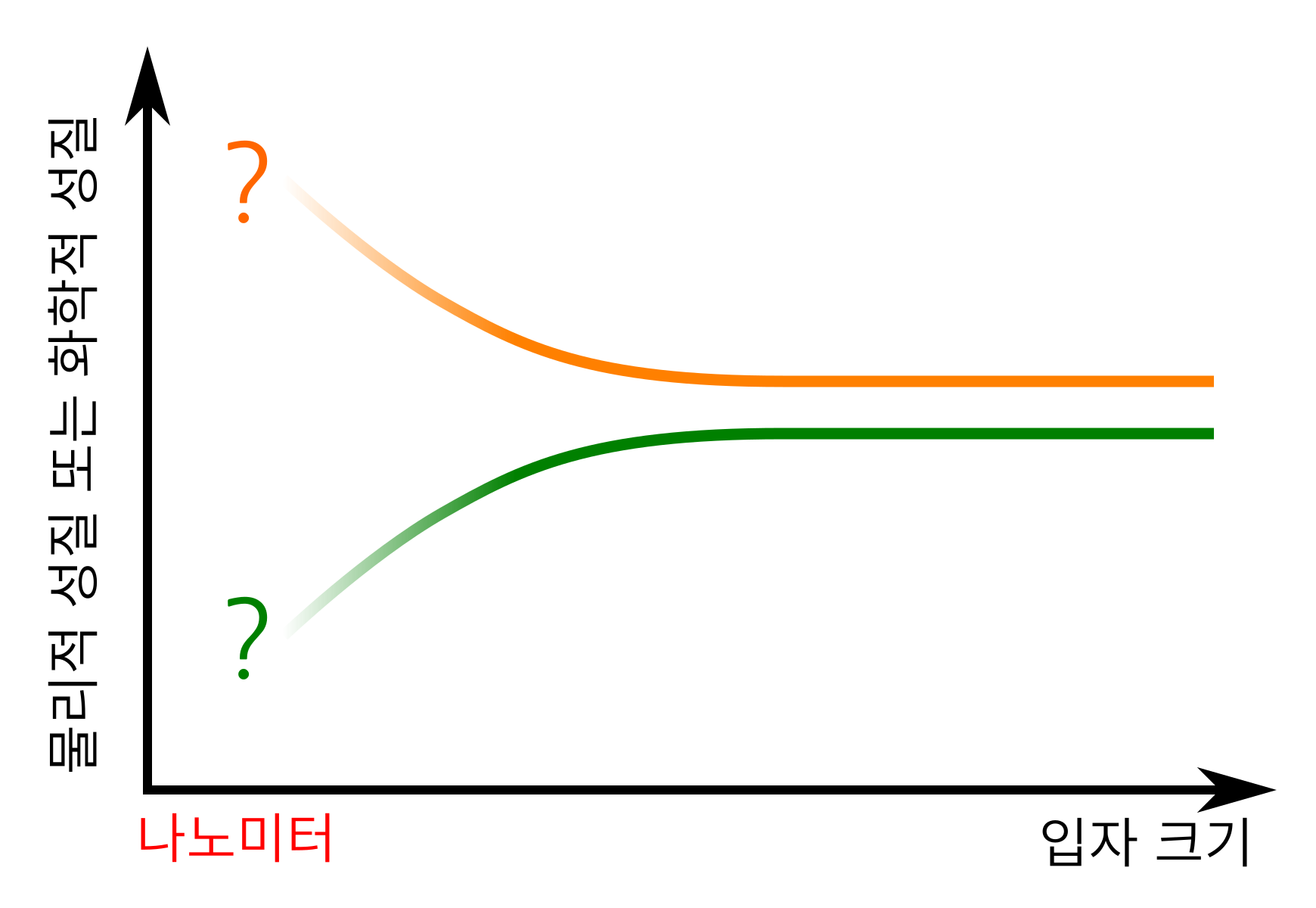
그림 7. 나노미터 크기가 되면 그보다 큰 크기의 입자와는 다른 성질의 변화 패턴이 나올 수 있다. 단순히 ‘크기’가 줄면서 변하는 성질의 연장선상에 있지 않은 경우가 많다.